cs231n 보충 자료 모아놓은 글

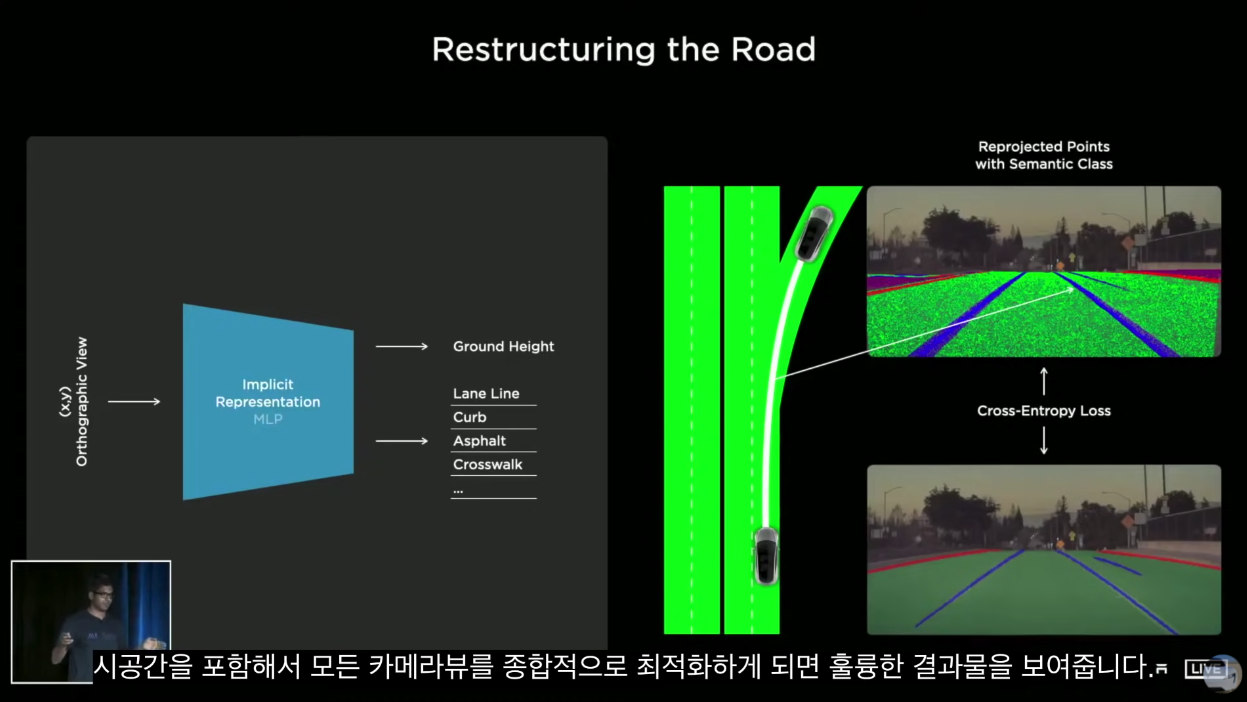
joint 결합확률은 product 와 같다!

이 부분은 몰랐던 부분이다 

 

Many authors use the term “cross-entropy” to identify specifically the negative log-likelihood of a Bernoulli or softmax distribution, but that is a misnomer. Any loss consisting of a negative log-likelihood is a cross-entropy between the empirical distribution defined by the training set and the probability distribution defined by model. For example, mean squared error is the cross-entropy between the empirical distribution and a Gaussian model.

 

크로스 엔트로피 단어를 사용하는 것은 잘못되었다

NLL 을 이루고 있는 아무(어떠한,모든) loss 들도 cross entropy 입니다 

empirical 분포 와 모델에 의한 negative log likelyhood 사이의 cross entropy 다

mean squared error 는 empirical 과 가우시안 모델 사이의 크로스 엔트로피다.

 

 

likely function 을 maximum 으로 한다

 logarithm 함수는 Max 값의 위치를 바꾸지 않고, value 만 0~1 로 바꾼다

y 는 데이터, variance 에 의해 scaled 된 theta.

두번째 항은 occam 의 면도기 같은,,,,,,,,  log determinant 항이다

n1, n2 을 -로 돌리고(y축 반전) x,y 씩 밀면 컨볼루션임 (*의 의미)

 

 

 

marginal probability, joint probability

x2의 확률 * x2 를 받았을 때,  x1 일 확률  * x2를 받았을때 x3일 확률

이상하게 생긴 N 은 가우시안 분포를 의미 (누 라고 발음한다면)

x1,x2,x3 는 랜덤베리어블(랜덤변수) 이며 선형적으로 변환한 브이자 형태인 누1,누2,누3 는 가우시안 '랜덤베리어블' 이다

mean 인 뮤 = 0 로 둔다

x1 - w1x2 는 v1 와 독립이다. (conditional probability, x2 를 받았을때, x1 일 확률) 

x3 - w3x2 는 v3 와 독립이다. 

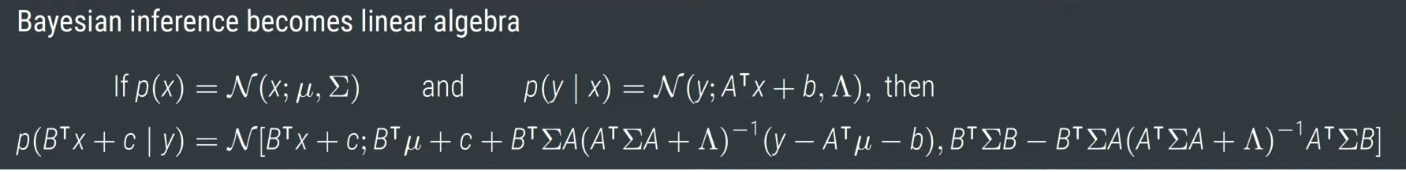
가우시안이 선형대수학으로 바뀔수 있어서 좋다는 뜻 

A : correct variable       (row vector) 

linear maps : P

x : three entries ( 행렬의  행들)

y : 출력값들중 하나 뽑는거

 

 

 

 

가우시안의 선형 프로젝션은 가우시안 분포이다

 

 

 

 

초록색 이 marginal probability . 각 랜덤변수에 대한  PDF 이다. (확률질량함수)

각 랜덤변수가 독립이면 이것들을 곱하면 joint probability 가 된다

 

 

 

Based on this “making model dumber” idea, I guess we can come up with other similar ways to avoid over-fitting, such as starting with a small network and gradually adding new neurons and connections to the network when more data is available. Or performing a pruning while training to get rid of connections that are close to zero.

So far we have demonstrated why sparsity can avoid over-fitting. But why adding an L1 norm to the loss function and forcing the L1 norm of the solution to be small can produce     sparsity?--> 뾰족함 정도로  직관적으로 해석    

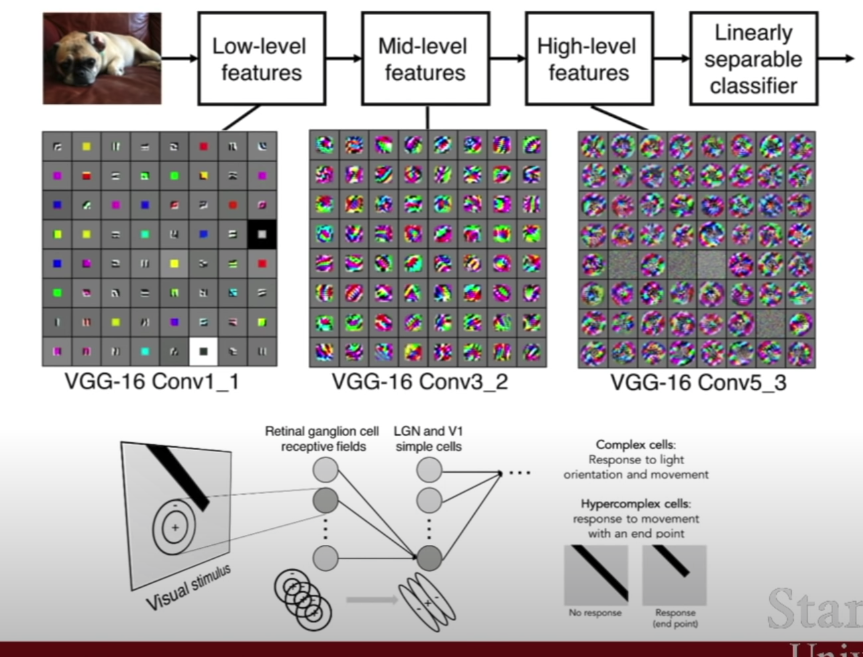
L2 norm

선형변환뒤 norm 도 변환됨

 

l2 norm 계산 완료

행렬식 값이 0이면 그 행렬의 역행렬은 존재하지 않는다는 것을 의미한다. 행렬식은 역행렬이 존재하는지 유무를 판별하는 특징이 있어서 결정하다(Determine)에서 유래해 영어로는 Determinant라는 용어로 불리는데, 아시아로 넘어오면서 행렬식(行列式)이라는 단어가 되었다

 

det(A) = 0의 경우

: A-1이 없다. 즉 뭉개진 차원을 다시 원래대로 돌릴 수 없다. 이는 다음에서 설명할, 한 행렬의 rank 갯수와도 연관이 있다.

orthogonal matrix = g   (직교화된) 

matrix = A  (n개의 column 을 가진,  직교화  안된 ) 

a1 이 밑에 깔린 선 a2 가 살짝 위로 간 선 그러면 다른 방향(A2) 가 살짝 생긴다

그래서 tiny 한 저 y 축 값을 만들기 위해 A2의 norm 으로 나눠준다!

https://ocw.mit.edu/courses/mathematics/18-065-matrix-methods-in-data-analysis-signal-processing-and-machine-learning-spring-2018/video-lectures/lecture-11-minimizing-2016x2016-subject-to-ax-b/

Lecture 11: Minimizing ‖x‖ Subject to Ax = b | Video Lectures | Matrix Methods in Data Analysis, Signal Processing, and Mac

column exchange, column pivoting 

q1 , q2 는 unit vector 이다

y축의 값(새로운 축의) 은  = A2

작을 것이다

So let me just write down what you have to do in a different order. So this is now with column pivoting, column exchange, column pivoting allowed, or it's possible. So to make it possible, I have to find not only A2, the piece of little a2, I have to find a2, the piece. I'm just going to copy that. I have to take my second column, subtract off the q1 part. And that could be small. So I have to compare it with-- oh, I haven't written this page up. So I haven't got a notation in mind yet. I won't give it a name. I have to also compute at this step before deciding q2-- now I'm describing how to decide q2, the second vector. And I'm saying that the way to decide q2 is not only to take a piece of a2 but also the piece of a3. Look at this piece. And look at all the other pieces.

https://zerobone.net/blog/cs/gram-schmidt-orthogonalization/

Implementing and visualizing Gram-Schmidt orthogonalization

직교하게 만듬(plane 에 projection 해서 A3 알아냄...)

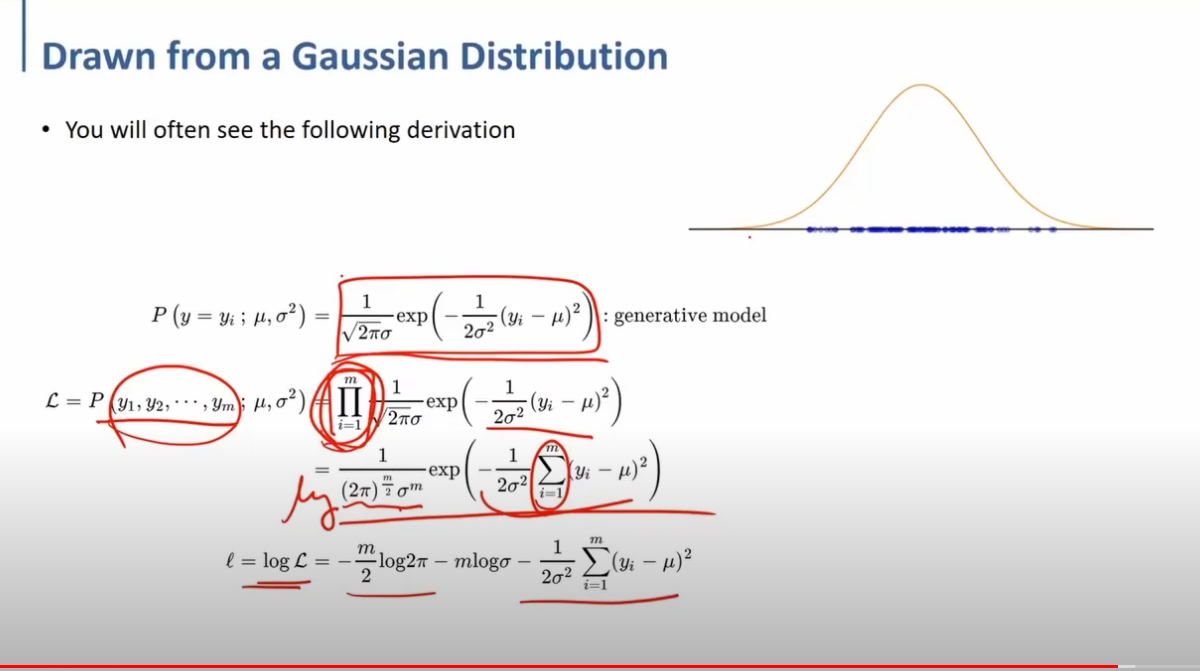
joint probability(결합확률분포) 

= > 각 데이터 포인트 y1,y2 들이 서로 독립이라  marginal probability 의 곱하기 가 된다