cs231n __ lecture( 10 ) LSTM과 Resnet 의 유사점

https://www.youtube.com/watch?v=EW08rD-GFh0

2

https://www.youtube.com/watch?v=EW08rD-GFh0

cs231n 9강에서의 편미분 총 6개의 독립파라미터를 가지고 있다.

 

i, f, o ,g 게이트 4개와, h(히든 스테이트), x(입력) 2개로 6개의 독립 파라미터를 구축하였다.

 

그중에 i, f, o 는 동일한 시그모이드 연산을 하였다. 자 6개의 term 중 비슷한거 3개를 찾아보자

내생각에는 2차 편미분항들이 3개로, 시그모이드 연산(0~1로 출력) 은 2차 편미분연산자(라플라시안) 과 비슷한 역할이라는 것을 추정할 수 있다.

 

위 사진을 바탕으로 각 게이트의  연산자들을  추정해보았다 

          라플라시안 연산자들              

   i                           input gate (x 에 대한 2 차 편미분)        

    f                    forget gate (x 에 대한 1차 편미분)            

         o                    output gate (x, y에 대한 2차 편미분)                    

 g   

          g   는 우리가 인풋 셀에 얼마나 적기를 바라는 지를 나타내는 것이다...

(y에  대한 2차 편미분)      

    c             cell state ( y 에 대한 1차 편미분)    (델 연산자)           

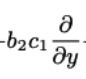
hidden state (상수항)

 

cell state 를  tanh 해주고, Output state 와 element wise operation(엘리먼트별 곱셈),요소별 곱셈

--> 셀 스테이트가 tanh 를 지나며 스칼라 값으로 변화???? 

 

해줘서 hiddenstate 를 얻어낸다

 

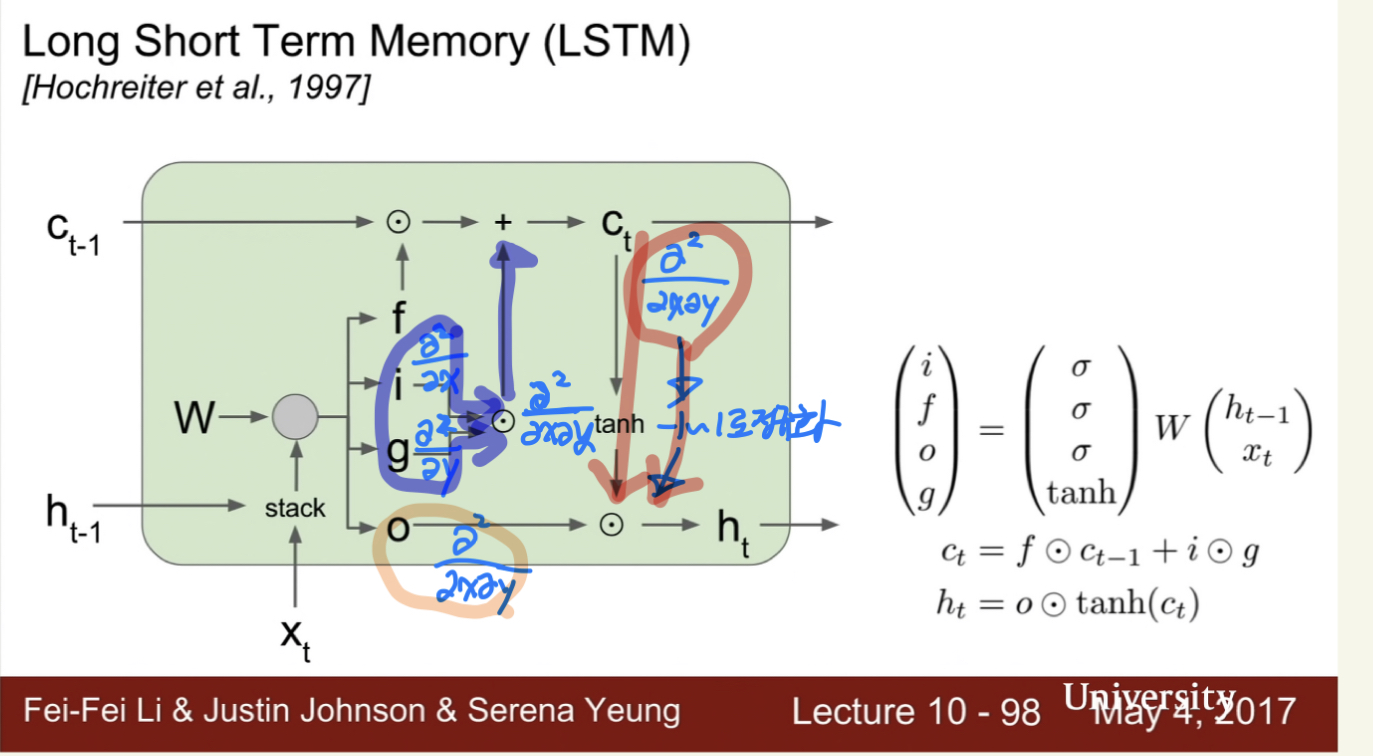
+연산을 쓰는  이유:

1차 편미분항,   2차 편미분 항을 섞어줌으로서 cell_state 가  스칼라값(차원 축소) 이 나옴

2차 편미분항까지 정규화해주기 위해서

 

tanh 쓰는이유 

1.    요소 별  곱을 위한 차원 축소(2차 편미분에서 스칼라로...)

2.     미리 더해진 2차 편미분항 까지 정규화해주기 위해서

 

그림 참고 

 

라플라시안 간략설명:

오목한점(최소점) 에서는 퍼지고 (+)

높은점(최고점)에서는 모아진다(벡터들이) (-) 

우리가 산 뿐 아니라, 바다에서도 최저점을 찾기 위해서는 이런 연산자가 필요하다.

어떻게 바다에서 gradient,기울기 를 찾겠는가?

입자가 파동을 치는 미시 세계,미시 과학에서 , 우리 모든 물체는 파동방정식으로 설명될 수 있다.

수학적인 증명들로 풀이한 6개의 독립파라미터 중 시그모이드만 3개 추리면

라플라시안 연산자가 3개 나오는 것이다... (Resnet 모델에 따르면)

 

 

 

 

 

시퀀스가 길기 때문에 우리가 역 전파를 하였을 때, 문제점이 생기는 것이라면 ( 저 산을 걸어내려가면서 산의 기울기만 보았던게(dradient) 우리가 그전에 했던 거라면, gradient 에 divergent 을 해서 연산자들을 3개 만들어서 우리는 문제를 해결하였다) 

Time domain 과 동시에 Frequency domain 을 생각 하여야 한다. 그래서 저 편미분항들이 나온것이고

자세한 사항은 다른글에 있다(cs231n 9강) 

동영상 강의에서도 Resnet 과 비슷한 점이 있다고 한다

element wise multipication >> full matrix 연산보다 좋음

백프로파게이션을 통해 gradient 계산 --> 문제 많음(그라디언트 폭발 혹은 소실 문제) 

4 개의 독립 파라미터 (x_t,

h_t,

z_t,

h_t(hat)

)