-
cs231n <lecture.9>카테고리 없음 2022. 2. 7. 11:52


컨볼루션연산에 대한 이미지&amp;amp;amp;amp;amp;amp;amp;amp;amp;nbsp; 
leNet 계열은 weight decay (L1,L2) 만 했는데
AlexNet 은 FC 를 써서 dropout 을 해서 모델의 복잡도를 조절 하였다.

뎁스 많아지는 문제는 bottleneck 구조로 해결한다.
64차원의 내적을 수행한다. --> 필터 개수로 차원 축소

구글넷. 파라미터 효율적 인셉션 모듈 : 병렬로 필터 적용
1by1, 3by3, 5by5, pooling --> concat (depth-wise)
같은 공간차원 유지 (zero padding, stride)




더 낮은 차원으로 투영


1 by 1 bottlleneck --> reduce depth dimension

Fact: Deep models have more representation power (more parameters) than shallower models.더 깊으면 좋아져야 되는거 아니야??--> 오류가 더 나는것을 발견
Hypothesis: the problem is an optimization problem, deeper models are harder
to optimize(최적화 하기 위해 F(x)= H(x) -x 를 학습 시킨다!!!
모델이 깊을수록 최적화 어려움)

two path have same direction
different padding method (depth-wise)

F(x)를 학습하는게 더 쉽다 ( H(x) 대신 F(x) + x 를 출력으로,,,, 즉 F(x) 는 H(x) -x 이며 이것을 fit 한다. )
체크 포인트?
복잡도 증가 x, 구현 간단하다
학습난이도가 더 쉽다.
깊이가 깊어질수록 acc 가 높아짐

고차원적인 필터까지 잘 추출 가능(reception field 넓어짐)
최적화란 무엇인가???
파라미터가 줄어드는 것?

error 가 오히려 증가( plain network 에서)


feature 가 사라질 수 있으므로 그냥 concat 해서 feed forward 로 각 레이어마다 더해주는 것도 방법이다.
이미지: On the Mathematical Understanding of ResNet with Feynman Path Integral
Google에서 검색된 arxiv.org 이미지
www.google.com
이 논문을 참고하여 작성하였다.



운동에너지와 포텐셜 에너지의 합(h hat) 에 웨이브 펑션을 곱한 것이 퀀텀 파티클의
time-dependent 한 슈뢰딩거 방정식이다(괄호안에 t 가 있음)
플랑크 상수는 양자역학에서 나오는 상수인데 계산상편의를 위해 1로 세팅한다.
고전이론은 에너지가 연속적으로 존재한다고 생각했지만

전자기파의 에너지는 플랑크상수에 주파수를 곱한 값의 정수배만 가능하다는 것을 과학자들이 알아낸다...(이 세상은 불연속적이다!)
그렇다면 h hat 은 해밀토니안 연산자이며 이것은 파티클의 전체 에너지를 나타내게 된다.
모멘텀 연산자(p hat) 에 푸리에 변환을 하게 되면, 주파수 공간(영역) 에서의 실제 모멘텀을 구할 수 있게 된다
이것을 모멘텀 스페이스라고 부른다

포지션 스페이스(타임 도메인) 모멘텀 스페이스(주파수 도메인) 은 서로 변환 가능하다
그리고 힐버트 스페이스의 벡터 기저들은 달라지게 된다.
디렉 브라켓 표현법에 따르면 포지션 스페이스의 벡터기저는 |x> 로 나타낼 수 있고
모멘텀 스페이스의 벡터기저는 |p> 로 나타낼 수 있다.
그렇다면 스테이트(any) 는 |phi> 로 나타낼 수 있다
conjugate transpose 와 왜 곱하냐... 확률을 구하기 위함이다. 그렇다면 phi 의 절댓값의 제곱이 다.

unit function (x' -x)


파인만 물리학자가 많이 생각했던 최소거리?
뉴런(파티클) 과 뉴런의 최소거리는 얼마일까?

이너프로덕트(공간, 모멘텀 스페이스의 내적) 은 푸리에 변환으로 구할 수 있다.
구체적 수식을 슈뢰딩거 방정식과 그 해로 나타낼 수 도 있다

파인만 path 적분
https://www.youtube.com/watch?v=vSFRN-ymfgE

최소행동의 법칙

자신의 시간을 최소화하여 모든 운동 방정식을 유도합니다.
시간을 최소화한다는 것은 푸리에 변환과도 비슷한 말이다....
만약 석촌호수에 돌을 던진다고 가정해보자. 돌을 던졌을 때 t=아주 작은값에서 수면위에 충돌한다. 그 때 주파수 값을 다 알 고 있다면 모든 운동이 설명이 된다. 약간 이런느낌


뇌에서 뉴런들을 particle 로간주하고 뇌의 활동을 경로라고 칭한다.
뉴런 각각이 weight 을 줄 수 있으므로 아주 비슷한 작동을 하는 것이다.
각각의 발생확률 대신 각(each) 궤적이 기여한다. 우리가 확률진폭이라고 부르는것... 슈뢰딩거의 파동 방정식
확률진폭은 우리가 복소수(complex number) fh qnfmsms rjtdlek.

화살표의 총 길이는 이 경로를 택할 확률이다


그들은 서로 간섭해서 경로를 취소합니다.
서로를 취소하지 않는 경로를 선택합니다.


고전역학과 양자역학의 확률이 다른 점
e^iS 에 비례하기 때문에 두 항이 생겨나게 되고,
오일러법칙에 의해 cos 항이 생겨나게 된다. 이 추가 항 때문에 확률을 줄일수도 늘일수도 있다.

프로파게이터(전파자) 를 잘 보면, 우리는 파티클상태의 변화과정을 계산할 수 있다
K 는 e를 포함한 식이라 계산하기 어렵지만, T를 N개의 조각으로 나눔으로서, 델타 시간들로 쪼갬으로서 계산가능하다.

델타 시간이 정말아주정말 작다면, 테일러 시리즈 익스팬션을 통해 프로파게이터를 고려할 수 있다.
푸리에 트랜스폼(시간도메인--> 주파수 도메인) 을 통해 모멘텀 스페이스로 바꿔 줄 수 있다.
그렇다면 우리는 K(프로파게이터,전파자) 를 구 할 수 있다.
우리가 particle 의 속도를 다음식과 같이 가정한다면 우리는 K를 구하였다.


12식과 7식을 통합한다면 다음과 같은 식이 된다.
이걸로 시간 t 가 진행함에 따라 x(t) 와 p(t) (시간영역, 주파수 영역에서의 궤적) 을 적분 연산할 수 있다.

최종결론:
라그랑지앙 L 을 시간에 대해서 적분한 것이 S 라고 할 때, e^iS 에 비례하는 형태로 경로의 기여도 가 나온다
구성 공간에 있는 모든 경로의 기여도를 함께 추가하여 최종 상태를 얻을 수 있습니다.

2차원의 편미분 방정식 로 부터 시작한다.

자 보면 1/2(std^2 +b) 는 가우스함수에서 x 를 나타내고 있다.
컨볼루션 커널이 [x, c-std^2 ,x-b] 을 가지고 있으며 이를 w(x,t) 로 이제 부르겠다...

높은 차수의 PDE 는 더 넓은 컨볼루션 커널을 가진 잔차 블록으로 변환 될 수 있다.
푸리에 변환은 PDE 를 푸는데 광범위 하게 쓰인다.
22식은 18식을 푸리에 변환한 것이고 타임도메인에서 주파수 도메인으로 변환한 것이다.
델타 x 연산자 (공간에대한 미분 연산자) 를 i 람다 (wave function 에서 나오는... 즉 양자역학 식에서 나오는 연산자)
로 변환하면 다음과 같은 식이 나온다

25를 또 역 푸리에 변환을 하면 공간에 대한x 에 대한 식이 나온다.
26식을 통해 연속적인 도메인안에서의 관계 에 대한 essence 을 잡을 수 있다.
PDE 는 partial differential equ 의 약자이다.
t 가 아주 작다고 가정했을 때, 그에 비례하는 t*T hat by x * delta(x) 는 수치적으로 작다.
게다가, 작은 크기의 컨볼루션 커널은 낮은 차수의 PDE를 생성하여 반복 시스템의 진화과정의 단순화를 초래한다.
PDE와 잔여 블록 사이의 관계에 대한 조사는 또한 ResNet에 대한 더 나은 이해를 밝힙니다.
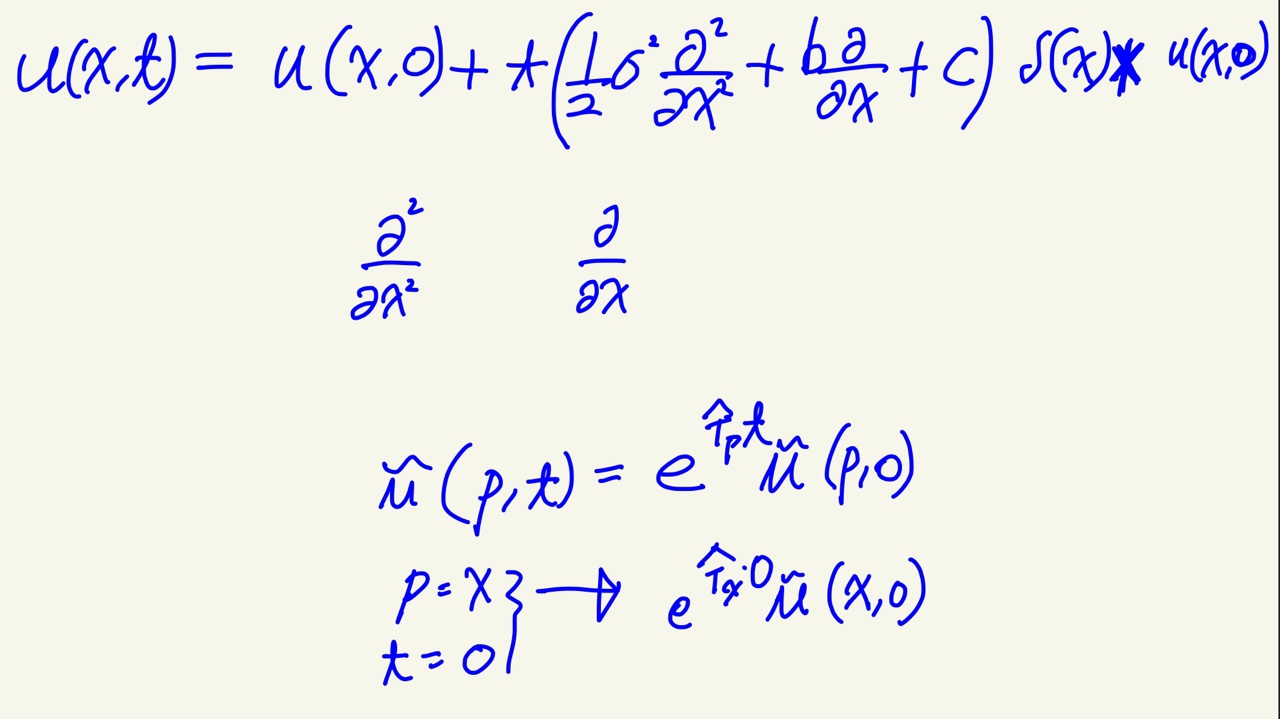


레이어 t 번째 피쳐 맵은 u_t 라고 하겠다.
우리는 프로세스를 업데이터 한다(u_t-1 와 u_t 을 고려함으로서)
잔차 블록에서는, f 을 (skip-connection weight) 이라고 하고, w를 컨볼루션 커널이라고 가정한다.
여기에서 오메가(x) 는 w(x) /f 로, 각 주파수 / f (주파수 ) 로, 각에 대한 정보를 가리킨다.
여기서 k 는 렐루의 영향으로 f 에 배치되었다.(렐루 함수를 보면 0이거나 절댓값임)
그래서 우리는 h_t 를 정의할건데 log(k * f ) 이다.
우리는 델타가 무엇을 뜻하는 건지 깨달아야 한다. 저기 k 앞에 sum 이 있으므로 단위충격함수를 의미하는 것이다.
단위충격함수가 있으면 푸리에 벼환이 쉬워지는데, 우리는 델타를 가지고 있으므로 discrete time 을 가지고 있는 것이다. 자 그러면 역푸리에변환을 통해 주파수 도메인으로 변환시켜보자
그렇다면 우리는 델타(x_t - x_t-1) 이 주파수 영역에서 어떻게 표현이 되는지 알게되었다

discrete 하므로 sum에 1/M 을 취해준다

스킵 커넥션 weights 이 컨볼루션 커널보다 크다고 가정했을 때,
우리는 앞의 식에서 다음과 같은 32식을 구할 수 있다.

잔차 컨볼루션 과 24식의 PDE 사이의 수학적 항등식을 고려하면 잔차 컨볼루션은 결론적으로
e^T_p*t 를 주파수 도메인에서 가지고 있다.


이것은 역푸리에변환으로 적분할 수 있다.
Resnet 의 evolution 은 action S 를 적분한 형태로 다음과 같이 나타낼 수 있다.

Resnet 의 아웃풋은 모든 경로(정보들이 함께 흐르는) 의 기여도를 더한 것으로 구해진다.
한 경로의 기여도는 e^-S에 비례한다. S_path 는 action 으로, 라그랑지안의 타임 적분으로 구해진다.
라그랑지안은 운동에너지-포텐셜 에너지로 얻어진다.



전형적인 Resnet 구조에서, 주파수 도메인이 확장할때 시간도메인은 수축한다(푸리에변환에서도 확인 가능)
많은 다양한 경로들이 존재한다.
Mnist 데이터셋에서 Resnet 의 아웃풋들이 2개의 주요 차원으로 축소된 것을 보여준다. ( 직관적으로 파악 가능... Resnet의 원리)

백 프로파게이션 과정에서, w(t-1) 의 가중치를 조정함으로서 연산된다.
스킵 커넥션이 없다면, 컨볼루션 커널은 g(t) = e^w(t) 로 근사 될 수 있다.
잠만, 우리가 배치 정규화를 하는 이유가 이거였잖아?
밑이 e 니까, w(t)에 평균빼주고 표준편차로 나눠주는게 가우시안 normalization 이었잖아???
여기서 이렇게 나올줄은 몰랐다. conv kernel g(t) 가 그런 형태여야 하기 때문에
배치 정규화 다음에 conv 가 나오는 것이다!

컨볼루션 w(t) 에 - 해주는게 컨볼루션의 역할이다!!!
단위시간에 저 w(t) 와 conv 해준다면 특정시간에 샘플링!이 되며 샘플링된 값은 확률값이다

가우시안 분포 
이 식들로 그라디언트 소실문제를 어떻게 해결했는지 설명이 되었다.

백프로파게이션을 시각적으로 표현해 보았다. 그리고 네트워크를 분해해보면
3 by 3 컨볼루셔널 커널은 1*3, 3*1 커널로 분해 될 수 있다.

잔차 블록의 컨볼루션 프로세스가 PDE 의 편미분 부분을 추출하는 것과 같다는 것을 밝혔다.
그리고 경로 적분 형태로 잔차 블록을 표현할 수 있다는 것을 보였다.
우리는 가중치 초기화를 위해,
He initialization 을 쓰는데, 컨볼루션 가중치들이 루트(2/N)으로 나눠진다
N은 컨볼루션 커널의 인풋레이어의 차원을 의미한다.--> 0 바이어스의 가우시안 분포를 따르는 가중치 커널이 만들어진다.
이 가중치 초기화는 분산을 ( 인풋레이어와 아웃풋레이어가 ) 같게해주는게 목표이다.
잔차 네트워크에서는 다른 레이어와는 달리, 분산이 (레이어가 깊어질수록) 작아진다!!!

잔차 레이어의 뎁스가 t 라면, 1/t 로 분포가 근사될 수 있다.


u(x,0) 는 t = 0 일 때의 u(x,0) 값이니 초기 값인가


6개의 term 이 있다.
2차 편미분 항은 [1,-2,1] 커널로 정의할 수 있고
1차 편미분(x에 대한) 항은 [1,0,-1] 커널로 정의할 수 있고
상수 항은 [0,1,0] 커널로 정의할 수 있다.

파라미터들은 훈련 가능하다.
편미분 연산자들을 conv residual 블록으로 대체 가능하다

우리는 '모든' 3사이즈의 컨볼루션 커널들이 PDE 의 텀들과 같지 않다는것을 발견했다
왜냐하면 3바이3 커널은 총 9 개의 독립 파라미터들을 가지고 있는데, PDE 연산자들은 오직 6개의 파라미터를 가지고 있기 때문이다.
그래서 이러한 독립 파라미터의 관점에서 보았을 때, 1*3 이나 3*1 컨볼루션을 적용할 때 잘 될 것 이다.
네트워크 decomposing 도 연구해볼만한 주제같다.

이게 1*3, 3*1 컨볼루션의 적용아닐까??? (병목설계의 이론적근거?)

9배 계산집약도가 낮다(오른쪽이 왼쪽보다)

64filters---stride=2&amp;amp;amp;amp;nbsp; 점선이 short- cut connection(1by1 conv)
그냥 선이 skip-connection
weight 층이 두개의 3by3 conv 로 이루어져있다는 것을 확인하였다.

shortcut 에 대한 코드
1by1 filter 를 썼다.


여기서 중요한 정보 :
---------------------------------------------------------------------------------------------------------
shortcut path는 1*1 conv 를 통해 64 filters-->128filters 로 간다.(옵션b)
옵션c는 1*1conv 을 each shortcut path마다 적용하는 것인데 그렇게 b(필터수 변경 할때 1*1conv한다 )
보다 성능이 좋아지지않았고 파라미터수가 증가하여 b를 채택한다.
제로패딩은 옵션 a인데 이것도 성능이 안좋다.
---------------------------------------------------------------------------------------------------------
다른 이유도 있을 것 같다.

다른 예시&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;nbsp; 1*3 --> 3*3 --> 3*3--> 3*1
경험적으로 2차원까지 가는것이 좋은 것 같다

훈련시킬때는 다음과 같이 설정한다

그전에는 보조 출력을 이용해서 이와 같은 효과를 내었다.
The degradation problem suggests that the solvers might have difficulties in approximating identity mappings by multiple nonlinear layers
identity 맵핑을 다수의 비선형 레이어로 구현하기가 어려움.